![]()
|
|
|
 |
|
|
ความสัมพันธ์ระหว่างแอททริบิวต์ในแต่ละรีเลชันแอททริบิวต์ (attribute) ในแต่ละรีเลชัน (relation) อาจมีความสัมพันธ์กันในลักษณะที่ เมื่อทราบค่าของแอททริบิวต์หนึ่งจะทำให้สามารถทราบค่าของแอททริบิวต์อื่น ๆ ในทูเพิล (tuple) เดียวกันของรีเลชันได้ ซึ่งความสัมพันธ์ระหว่างแอททริบิวต์ในแต่ละรีเลชันอาจจำแนกได้ 3 ลักษณะ คือ ความสัมพันธ์ระหว่าง แอททริบิวต์แบบฟังก์ชัน (functional dependency) ความสัมพันธ์ระหว่างแอททริบิวต์แบบหลายค่า (multivalued dependency) และความสัมพันธ์ระหว่างแอททริบิวต์แบบ Join (join dependency) 1. ความสัมพันธ์ระหว่างแอททริบิวต์แบบฟังก์ชันความสัมพันธ์ระหว่างแอททริบิวต์แบบฟังก์ชัน หรือ FD หมายถึง การที่ค่าของแอททริบิวต์หนึ่งหรือมากกว่าหนึ่งแอททริบิวต์ขึ้นไปที่ประกอบกันสามารถระบุค่าของแอททริบิวต์อื่น ๆ ในทูเพิลเดียวกันของ รีเลชันนั้นได้ โดยแอททริบิวต์หรือกลุ่มของแอททริบิวต์ที่เป็นตัวระบุค่าของแอททริบิวต์อื่น ๆ เรียกว่า Determinant และแอททริบิวต์อื่น ๆ ที่ถูกระบุค่า เรียกว่า Dependent
ในแผนภาพความสัมพันธ์ระหว่างแอททริบิวต์แบบฟังก์ชัน (functional dependency diagram) หรือ FD ไดอะแกรมใช้สัญลักษณ์ดังนี้ หมายความว่า หากทราบค่าของแอททริบิวต์ A จะสามารถทราบค่าของแอททริบิวต์ B ได้โดย A ซึ่งเรียกว่า Determinant อาจเป็นแอททริบิวต์หนึ่งหรือกลุ่มของแอททริบิวต์ที่นำมาประกอบกันก็ได้ และ B ซึ่งเรียกว่า Dependent จะเป็นแอททริบิวต์อื่น ๆ ในทูเพิลเดียวกันของรีเลชันนั้น เพื่อให้เข้าใจความสัมพันธ์ระหว่างแอททริบิวต์แบบฟังก์ชันดียิ่งขึ้น ในที่นี้ขอนำตัวอย่างมาประกอบดังนี้
ภาพที่ 4.1รีเลชันอาจารย์ที่ปรึกษารีเลชันอาจารย์ที่ปรึกษามีความสัมพันธ์ระหว่างแอททริบิวต์แบบฟังก์ชันดังนี้
เขียน FD ไดอะแกรมได้ดังนี้
หมายความว่า หากระบุค่าของรหัสนักศึกษาคนใดก็จะสามารถทราบชื่ออาจารย์ที่ปรึกษาของ นักศึกษาคนนั้นได้ เช่น ถ้าระบุค่าของ Determinant หรือ รหัสนักศึกษา คือ 41012451 จะทำให้ทราบค่าของ Dependent หรือ ชื่ออาจารย์ที่ปรึกษา คือ ศิริชัย ศรีพรหม ได้ ในทางตรงกันข้าม หากทราบค่าของ Dependent อาจไม่สามารถระบุค่าของ Determinant ก็ได้ เช่น ถ้าระบุค่าของชื่ออาจารย์ที่ปรึกษา คือ ศิริภัทรา เหมือนมาลัย จะพบว่าค่าของรหัสนักศึกษามี 2 ค่า คือ 41010943 และ 41013780 เนื่องจากนักศึกษาทั้งสองคนมีอาจารย์ที่ปรึกษาคนเดียวกัน ดังนั้น จึงกล่าวได้ว่า ค่าของ Determinant สามารถระบุค่าของ Dependent ได้ แต่ค่าของ Dependent อาจไม่สามารถระบุค่าของ Determinant ที่ชัดเจนได้ หากต้องการให้แอททริบิวต์ชื่ออาจารย์ที่ปรึกษาเป็น Determinant เพื่อให้สามารถระบุค่าของ Dependent คือ รหัสนักศึกษา ได้ จะต้องกำหนดให้ชื่ออาจารย์ที่ปรึกษาของนักศึกษาแต่ละคนไม่ซ้ำกัน นั่นคือ หากระบุค่าของรหัสนักศึกษาคนใดก็จะสามารถทราบชื่ออาจารย์ที่ปรึกษาของนักศึกษาคนนั้นได้ และในทางตรงกันข้าม หากทราบค่าของชื่ออาจารย์ที่ปรึกษาคนใดก็จะสามารถระบุค่าของรหัสนักศึกษาใน การปรึกษาของอาจารย์คนนั้นได้ ซึ่งรูปแบบของความสัมพันธ์จะเป็นดังนี้ รีเลชันอาจารย์ที่ปรึกษามีความสัมพันธ์ระหว่างแอททริบิวต์แบบฟังก์ชันดังนี้
หรืออาจเขียนได้ดังนี้
เขียน FD ไดอะแกรมได้ดังนี้
ภาพที่ 4.2รีเลชันนักศึกษารีเลชันนักศึกษามีความสัมพันธ์ระหว่างแอททริบิวต์แบบฟังก์ชันดังนี้
เขียน FD ไดอะแกรมได้ดังนี้
หมายความว่า หากระบุรหัสนักศึกษาคนใดก็จะสามารถทราบชื่อ นามสกุล และวัน/เดือน/ปีเกิด ของนักศึกษาคนนั้นได้ เช่น ถ้าระบุค่าของ Determinant หรือ รหัสประจำตัว คือ 41012147 จะทำให้ทราบค่าของ Dependent หรือแอททริบิวต์อื่น ๆ ได้ดังนี้
ภาพที่ 4.3รีเลชันอาจารย์ผู้สอนรีเลชันอาจารย์ผู้สอนมีความสัมพันธ์ระหว่างแอททริบิวต์แบบฟังก์ชันดังนี้
เขียน FD ไดอะแกรมได้ดังนี้
หมายความว่า หากระบุค่าของรหัสชุดวิชาและหมู่เรียนใดก็จะสามารถทราบชื่ออาจารย์ผู้สอนในรหัสชุดวิชาและหมู่เรียนนั้น ๆ ได้ เช่น ถ้าระบุค่าของ Determinant หรือ รหัสชุดวิชา คือ 999211 และหมู่เรียน คือ 712 จะทำให้ทราบค่าของ Dependent หรือ ชื่ออาจารย์ผู้สอน คือ ศิริชัย ศรีพรหม เมื่อกล่าวถึงความสัมพันธ์ระหว่างแอททริบิวต์มักจะเกี่ยวข้องกับคีย์ (key) เนื่องจากคุณสมบัติของคีย์หลัก (primary key) คือ แอททริบิวต์ที่มีค่าเป็นเอกลักษณ์หรือมีค่าไม่ซ้ำซ้อนกัน (unique) ทำให้สามารถระบุค่าของแอททริบิวต์อื่นในทูเพิลหนึ่ง ๆ ได้ โดยแอททริบิวต์ที่มีคุณสมบัติเป็นคีย์หลักอาจเป็นกลุ่มของ แอททริบิวต์ที่นำมาประกอบกันเพื่อให้มีค่าเป็นเอกลักษณ์ก็ได้ ซึ่งกลุ่มของแอททริบิวต์ดังกล่าวเรียกว่า คีย์ผสม (composite key) จากภาพที่ 4.2 รีเลชันนักศึกษามีเพียงหนึ่งแอททริบิวต์ที่มีคุณสมบัติเป็นคีย์หลัก คือ รหัสนักศึกษา หากระบุรหัสนักศึกษาคนใดก็จะสามารถทราบชื่อ นามสกุล และวัน/เดือน/ปีเกิด ของนักศึกษาคนนั้นได้ และจากภาพที่ 4.3 รีเลชันอาจารย์ผู้สอนมีกลุ่มของแอททริบิวต์ที่ประกอบกันและมีคุณสมบัติเป็นคีย์หลัก คือ รหัสชุดวิชาและหมู่เรียน หากระบุค่าของรหัสชุดวิชาและหมู่เรียนใดก็จะสามารถทราบชื่ออาจารย์ผู้สอนในรหัส ชุดวิชาและหมู่เรียนนั้น ๆ ได้ ดังนั้น จึงกล่าวได้ว่า คีย์หลักและคีย์ผสมเป็น Determinant ที่สามารถระบุค่าของแอททริบิวต์อื่น ๆ ในทูเพิลเดียวกันของรีเลชันนั้นได้ ทั้งนี้ ความสัมพันธ์ระหว่างแอททริบิวต์แบบฟังก์ชันสามารถจำแนกได้ 3 แบบ คือ ความสัมพันธ์ระหว่างแอททริบิวต์แบบทั้งหมด (fully functional dependency) ความสัมพันธ์ระหว่างแอททริบิวต์แบบ บางส่วน (partial dependency) และความสัมพันธ์ระหว่างแอททริบิวต์แบบ Transitive (transitive dependency) 1. ความสัมพันธ์ระหว่างแอททริบิวต์แบบทั้งหมดความสัมพันธ์ระหว่างแอททริบิวต์แบบทั้งหมด หมายถึง การที่แอททริบิวต์ซึ่งเป็น Determinant มีขนาดเล็กที่สุด และสามารถระบุค่าของแอททริบิวต์อื่น ๆ ที่เป็น Dependent ได้อย่างชัดเจน ตัวอย่างเช่น
รีเลชันนักศึกษามีความสัมพันธ์ระหว่างแอททริบิวต์แบบฟังก์ชันดังนี้
หากทราบค่าของ Determinant คือ รหัสนักศึกษาคนใดก็จะสามารถทราบค่าของ Dependent หรือแอททริบิวต์อื่น ๆ ในทูเพิลเดียวกัน คือ ชื่อ นามสกุล และวัน/เดือน/ปีเกิด ของนักศึกษาคนนั้นได้ ดังนั้น แอททริบิวต์ชื่อ นามสกุล และวัน/เดือน/ปีเกิด จึงมีความสัมพันธ์ระหว่างแอททริบิวต์แบบทั้งหมดกับ แอททริบิวต์รหัสนักศึกษา
รีเลชันอาจารย์ผู้สอนมีความสัมพันธ์ระหว่างแอททริบิวต์แบบฟังก์ชันดังนี้
หากทราบค่าของ Determinant คือ รหัสชุดวิชาและหมู่เรียนใดก็จะสามารถทราบค่าของ Dependent หรือแอททริบิวต์อื่น ๆ ในทูเพิลเดียวกัน คือ ชื่ออาจารย์ผู้สอนในรหัสชุดวิชาและหมู่เรียนนั้นได้ ดังนั้น แอททริบิวต์ชื่ออาจารย์ผู้สอนจึงมีความสัมพันธ์ระหว่างแอททริบิวต์แบบทั้งหมดกับแอททริบิวต์รหัส ชุดวิชาและหมู่เรียน 2. ความสัมพันธ์ระหว่างแอททริบิวต์แบบบางส่วนความสัมพันธ์ระหว่างแอททริบิวต์แบบบางส่วน จะเกิดขึ้นได้เมื่อรีเลชันหนึ่ง ๆ มีคีย์หลักเป็นคีย์ผสม และแอททริบิวต์บางส่วนของคีย์หลักสามารถระบุค่าของแอททริบิวต์อื่น ๆ ในทูเพิลเดียวกันที่ไม่ใช่คีย์หลัก (non-key attribute) ของรีเลชันได้ นั่นคือ หากทราบค่าใดค่าหนึ่งของบางแอททริบิวต์ที่เป็น Determinant ก็จะทำให้ทราบค่าของแอททริบิวต์อื่น ๆ ที่เป็น Dependent ได้ ตัวอย่างเช่น รีเลชันการลงทะเบียนประกอบด้วย แอททริบิวต์รหัสนักศึกษา รหัสชุดวิชา ชื่อชุดวิชา และหมู่เรียน โดยมีแอททริบิวต์รหัสนักศึกษาและรหัสชุดวิชาประกอบกันเป็นคีย์หลัก
ภาพที่ 4.4รีเลชันการลงทะเบียนรีเลชันการลงทะเบียนมีความสัมพันธ์ระหว่างแอททริบิวต์แบบฟังก์ชันดังนี้
เขียน FD ไดอะแกรมได้ดังนี้
จากภาพ รีเลชันการลงทะเบียนมีแอททริบิวต์รหัสนักศึกษาและรหัสชุดวิชาประกอบกันเป็นคีย์หลักหรือ Determinant ที่สามารถระบุค่าของ Dependent หรือแอททริบิวต์อื่น ๆ ในทูเพิลเดียวกัน คือ ชื่อชุดวิชาและหมู่เรียน ได้ ขณะเดียวกัน รีเลชันการลงทะเบียนมีความสัมพันธ์ระหว่างแอททริบิวต์แบบบางส่วนเกิดขึ้น เนื่องจากแอททริบิวต์รหัสชุดวิชาซึ่งเป็นส่วนประกอบหนึ่งของคีย์หลักสามารถระบุค่าของชื่อชุดวิชาซึ่งเป็นแอททริบิวต์ที่ไม่ใช่คีย์หลักของรีเลชันได้ ซึ่งความสัมพันธ์ในลักษณะดังกล่าวนี้อาจก่อให้เกิดปัญหาเรื่องความซ้ำซ้อนในการปรับปรุงข้อมูลได้ 3. ความสัมพันธ์ระหว่างแอททริบิวต์แบบ Transitiveแม้ว่าแอททริบิวต์ที่มีคุณสมบัติเป็นคีย์หลักจะสามารถระบุค่าของแอททริบิวต์อื่น ๆ ในทูเพิลเดียวกันของรีเลชันได้ แต่ทว่าในบางรีเลชันที่มีการออกแบบไม่เหมาะสม อาจมีแอททริบิวต์อื่นที่ไม่ใช่คีย์หลักแต่สามารถระบุค่าของแอททริบิวต์อื่น ๆ ในทูเพิลเดียวกันของรีเลชันได้เช่นกัน ลักษณะของความสัมพันธ์ดังกล่าวนี้เรียกว่า ความสัมพันธ์ระหว่างแอททริบิวต์แบบ Transitive
ภาพที่ 4.5รีเลชันที่ปรึกษาตัวอย่างเช่น รีเลชันที่ปรึกษาประกอบด้วย แอททริบิวต์รหัสนักศึกษา ชื่อนักศึกษา รหัสอาจารย์ และชื่ออาจารย์ที่ปรึกษา โดยมีแอททริบิวต์รหัสนักศึกษาเป็นคีย์หลัก รีเลชันที่ปรึกษามีความสัมพันธ์ระหว่างแอททริบิวต์แบบฟังก์ชัน ดังนี้
เขียน FD ไดอะแกรมได้ดังนี้ 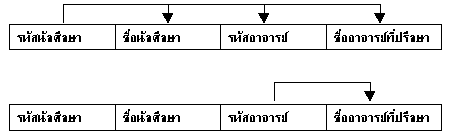 จากภาพ รีเลชันที่ปรึกษามีแอททริบิวต์รหัสนักศึกษาเป็นคีย์หลักหรือ Determinant ที่สามารถระบุค่าของ Dependent หรือแอททริบิวต์อื่น ๆ ในทูเพิลเดียวกัน คือ ชื่อนักศึกษา รหัสอาจารย์ และชื่ออาจารย์ที่ปรึกษาได้ ในขณะเดียวกัน รีเลชันที่ปรึกษามีความสัมพันธ์ระหว่างแอททริบิวต์แบบ Transitive เกิดขึ้น เนื่องจากรหัสอาจารย์ซึ่งเป็นแอททริบิวต์ที่ไม่ใช่คีย์หลักสามารถระบุค่าของแอททริบิวต์อื่นๆ ในทูเพิล เดียวกัน คือ ชื่ออาจารย์ที่ปรึกษา ได้ 2. ความสัมพันธ์ระหว่างแอททริบิวต์แบบหลายค่าความสัมพันธ์ระหว่างแอททริบิวต์แบบหลายค่า หรือ MVD จะเกิดขึ้นได้เมื่อรีเลชันหนึ่ง ๆ ประกอบด้วยสามแอททริบิวต์ขึ้นไป และแอททริบิวต์ที่เป็น Determinant สามารถระบุค่าของแอททริบิวต์อื่นที่เป็น Dependent ได้มากกว่าหนึ่งค่า หรือ ข้อมูลของแอททริบิวต์ที่เป็น Dependent จะเป็นกลุ่มของข้อมูล ความสัมพันธ์ระหว่างแอททริบิวต์แบบหลายค่าสามารถใช้สัญลักษณ์ ในการสื่อความหมาย ได้ดังนี้
หมายความว่า หากทราบค่าของแอททริบิวต์ A หนึ่งค่าจะสามารถทราบค่าของแอททริบิวต์ B ได้หลายค่า และเมื่อทราบค่าของแอททริบิวต์ A หนึ่งค่าจะสามารถทราบค่าของแอททริบิวต์ C ได้หลายค่า เพื่อให้เข้าใจความสัมพันธ์ระหว่างแอททริบิวต์แบบหลายค่าดียิ่งขึ้น ในที่นี้ขอนำตัวอย่างมาประกอบดังนี้ ตัวอย่างเช่น รีเลชันการสอน-การปรึกษาประกอบด้วย แอททริบิวต์รหัสอาจารย์ รหัสชุดวิชาที่สอน และรหัสนักศึกษาในการปรึกษา โดยมีแอททริบิวต์รหัสอาจารย์ รหัสชุดวิชาที่สอน และรหัสนักศึกษาใน การปรึกษาประกอบกันเป็นคีย์หลัก
ภาพที่ 4.6รีเลชันการสอน-การปรึกษาจากภาพ รีเลชันการสอน-การปรึกษามีแอททริบิวต์รหัสอาจารย์ รหัสชุดวิชาที่สอน และรหัส นักศึกษาในการปรึกษาประกอบกันเป็นคีย์หลัก โดยอาจารย์แต่ละคนจะสอนอย่างน้อย 1 ชุดวิชา ซึ่งบางคนอาจสอนชุดวิชาเดียวกันก็ได้ ขณะเดียวกันอาจารย์บางคนอาจมีนักศึกษาในการปรึกษาได้มากกว่า 1 คน โดยรหัสนักศึกษาในการปรึกษากับรหัสชุดวิชาที่สอนไม่มีความสัมพันธ์กันเลย รีเลชันการสอน-การปรึกษามีความสัมพันธ์ระหว่างแอททริบิวต์แบบหลายค่า ดังนี้
จากรีเลชัน หมายความว่า หากระบุค่าของรหัสอาจารย์หนึ่งค่าก็จะสามารถทราบรหัสชุดวิชาที่สอนได้หลายค่า เช่น ถ้าระบุค่าของรหัสอาจารย์ คือ Q1035 จะทำให้ทราบค่าของรหัสชุดวิชาที่สอน คือ 729101, 729104 และ 999211 และในขณะเดียวกัน หากระบุค่าของรหัสอาจารย์หนึ่งค่าก็จะสามารถทราบรหัสนักศึกษาในการปรึกษาได้หลายค่า เช่น ถ้าระบุค่าของรหัสอาจารย์ คือ Q1059 จะทำให้ทราบค่าของรหัสนักศึกษาในการปรึกษา คือ 41010703 และ 41013327 การที่รีเลชันเกิดความสัมพันธ์ในลักษณะดังกล่าวนี้ได้ เนื่องจากมีการนำแอททริบิวต์สามแอททริบิวต์ คือ รหัสอาจารย์ รหัสชุดวิชาที่สอน และ รหัสนักศึกษาในการปรึกษา มาไว้ในรีเลชันเดียวกัน โดยแอททริบิวต์รหัสอาจารย์มีความสัมพันธ์กับแอททริบิวต์รหัสชุดวิชาที่สอนและรหัสนักศึกษาในการปรึกษาเท่านั้น หากทว่าแอททริบิวต์รหัสชุดวิชาที่สอนและรหัสนักศึกษาในการปรึกษาไม่มีความสัมพันธ์ต่อกันเลย เมื่อทั้งสามแอททริบิวต์มาปรากฏอยู่ในรีเลชันเดียวกัน จึงทำให้เกิดค่าของข้อมูลที่ซ้ำซ้อนกันเป็นปัญหาต่อการปรับปรุง การเพิ่ม หรือการลบข้อมูลได้ 3. ความสัมพันธ์ระหว่างแอททริบิวต์แบบ Joinความสัมพันธ์ระหว่างแอททริบิวต์แบบ Join เป็นกฎเกณฑ์ที่สำคัญประการหนึ่งในการจำแนกรีเลชัน โดยรีเลชันใด ๆ จะมีความสัมพันธ์ระหว่างแอททริบิวต์แบบ Join เกิดขึ้นได้ก็ต่อเมื่อ รีเลชันนั้น ๆ สามารถจำแนกออกเป็นรีเลชันย่อยได้ และเมื่อนำรีเลชันย่อยที่จำแนกออกมาเหล่านั้นมารวมกันจะต้องได้รีเลชันกลับไปเหมือนเดิมเสมอ ตัวอย่างเช่น รีเลชันที่ปรึกษาประกอบด้วย แอททริบิวต์รหัสนักศึกษา ชื่อนักศึกษา รหัสอาจารย์ และชื่ออาจารย์ที่ปรึกษา โดยมีแอททริบิวต์รหัสนักศึกษาเป็นคีย์หลัก
ภาพที่ 4.7 ความสัมพันธ์ระหว่างแอททริบิวต์แบบ Join ของรีเลชันที่ปรึกษารีเลชันที่ปรึกษาสามารถจำแนกเป็นรีเลชันย่อยได้ 3 รีเลชัน คือ รีเลชันนักศึกษา รีเลชันอาจารย์ ที่ปรึกษา และรีเลชันนักศึกษา-อาจารย์
เมื่อนำรีเลชันย่อยทั้งสามมารวมกัน จะได้รีเลชันเหมือนรีเลชันที่ปรึกษาเช่นเดิม ดังนั้น จึงกล่าวได้ว่า รีเลชันที่ปรึกษามีความสัมพันธ์ระหว่างแอททริบิวต์แบบ Join เนื่องจาก รีเลชันที่ปรึกษาสามารถจำแนกออกเป็นรีเลชันย่อยได้ และเมื่อนำรีเลชันย่อยที่จำแนกออกมาเหล่านั้นมารวมกันก็จะได้รีเลชันที่ปรึกษาเหมือนเดิม
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|